利用closure這個特色來實作memoization以提高執行效能

因為前文所述的例子，讓我們覺得 closure 好像是一種很多餘的東西，只會害我們出錯，但其實是我們沒有好好讀書理解，我始終覺得每種程式語言的設計，當時設計者的取捨，一定都是有原因的，不是說設計出來的東西一定都是好的，但我相信都是有原因的，就看我們有沒有好好的去意會而已。

今天所有的資料內容都是來自：Javascript: The Good Parts
好書，一定要細細讀過。
Fibonacci numbers 怎麼算？

什麼是 Fibonacci numbers? 事關可愛的兔子，但有興趣的自己看： wiki。

在數學上來說就是：
F(0)=0
F(1)=1
F(n)=F(n-1)+F(n-2)

例如 F(3) = F(2) + F(1) = (F(1)+F(0)) + F(1) = 2
F(4) = F(3) + F(2)
= (F(2)+F(1)) + (F(1)+F(0))
= ((F(1)+F(0))+F(1)) + (F(1)+F(0))
= 3

要實作這個程式，也沒有很難，大家應該可以藉由上面的舉例發現，其實一直都在做重復的動作，所以用遞迴就可以了，Fibonacci 也一直都是遞迴很好的練習題。

var counter = 0;
var fibonacci = function(n){
  counter++;
  return n<2 ? n : fibonacci(n-1) + fibonacci(n-2); 
  // 這裡會遞迴呼叫兩次 fibonacci
};

for(var i=0; i<=10; i++){
  console.log(i, fibonacci(i));
}

console.log('call fibonacci:', counter);

這邊我們跑一個迴圈以得到一個 Fibonacci 數列，也特意放上一個 counter 計算跑了幾次。程式執行後，會發現總共執行了 453 次，扣掉我們用 for 迴圈呼叫的 11 次，遞迴共呼叫了 442 次。嗯，這數字好像太多了一點...

如果只計算 F(10) 呢？ 光是計算一個 F(10) 也需要遞迴呼叫 176 次。

我們再回到基本定義去看：
F(10) = F(9) + F(8)
= (F(8)+F(7)) + (F(7)+F(6))
= ...
這邊有沒有發現，有許多的重復計算，光是這樣拆解個兩次，就可以看到 F(8) 被計算了兩次，更何況是愈小的數字...

那能不能把這些計算過的儲存起來呢？這樣就不用再算啦！是的，沒有錯，有一種技巧叫做 Memoization，來看一下 wiki 的解釋：

In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs.

白話一點，就是我們剛剛想要做的事情：記憶前幾次計算過的結果，避免重復的計算，藉此來提高運算速度。

這種技巧跟程式語言沒有關係，但是，在 javascript 中有 closure 這種東西，在做「記憶」這件事情上就顯得非常方便。

我們直接看 Javascript: The Good Parts 中的程式碼：

var counter = 0;
var fibonacci = function(){
    var memo = [0, 1];
    var fib = function(n){
    counter++;
    var result = memo[n];
    if(typeof result !== 'number'){
      result = fib(n-1) + fib(n-2);
      memo[n] = result;
    }
    return result;
  };
  return fib;
};

var f = fibonacci();
for(var i=0; i<=10; i++){
  console.log(i, f(i));
}
console.log(counter);

在分析前，我們先看一下 counter 下降到多少，非常令人驚訝的是，counter 只有 29，扣除 for 迴圈呼叫的 11 次，遞迴呼叫的次數就僅剩 18 次，優化前遞迴呼叫次數是 442，18 比 442 有沒有很吸引人呢。

就算僅計算 F(10)，memoization 版程式只需要遞迴呼叫 18 次，比起改良前的 176，也是相當驚人。另外，大家有沒有發現，在 memoization 版中，迴圈計算 F(0)~F(10)的遞迴呼叫次數竟然跟僅計算 F(10) 一樣，如果大家理解 memoization 的精神的話，應該不難猜到為什麼。

現在我們來解析一下程式碼。

[code]
var fibonacci = function(){
    var memo = [0, 1];  //  負責記憶的陣列
    var fib = function(n){
    // 每次計算前都看一下，這次要計算的值有沒有在 memo 這個陣列中
    // 有的話表示已經計算過，就直接回傳。
    // 沒有的話，就開始計算，並將計算結果存(記憶)起來。
    var result = memo[n]; 
    if(typeof result !== 'number'){
      result = fib(n-1) + fib(n-2);
      memo[n] = result;
    }
    return result;
  };
  return fib;
};

// 執行過這行後，也就是呼叫了fibonacci這個函式
// 這個函式回傳的是fib這個函式，記得，這個時候 fib 並沒有被執行
// 而 memo 是 fibonacci 的一個區域變數
var f = fibonacci(); 

// 執行 f(10) 的這時候才是真的去執行 fib，fib 有用到 memo
// 這時候如果放斷點的話，會看到 memo 會被放在 closure 這個區中
// 記得，closure 是用參考的方式在存取的
f(10); 

我們用一個小一點的數字來分析

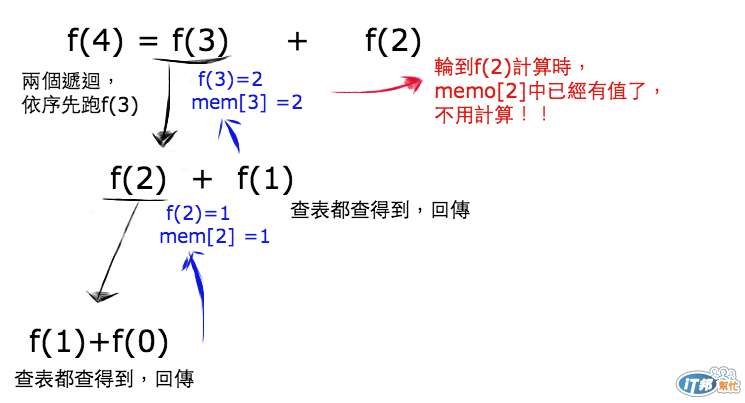
那為什麼跑 0~10 計算這 11 個的 fibonacci number 與只計算 f(10)的遞迴呼叫次數是一樣多呢？因為 f(10)需要遞迴到最深，當要計算 F(10) = F(9)+F(8)時，需要遞迴呼叫 2 次函式，但當真的要開始執行F(9)與F(8)時，就會發現 memo[9] 與 memo[8]已經有值了，所以就不需要再往下計算了。這邊，建議大家拿起紙筆自己試著跑一次看看，很有趣喔。

最後，Javascript: The Goode Parts 還將這個技巧整理出一個通用性的函式：

var memoizer = function(memo, fundamental){
  var shell = function(n){
    var result = memo[n];
    if(typeof result === 'undefined'){
      result = fundamental(shell, n);
      memo[n] = result;
    }
    return result;
  };
  return shell;
};
// 使用範例
var fibonacci = memoizer([0,1], function(shell, n){ 
        return shell(n-1)+ shell(n-2);
    });

var factorial = memoizer([1,1], function(shell, n){
	return n*shell(n-1);
    });

這邊真的很好玩，大家可以花點時間好好地理解下，我對這個方法真的是相逢恨晚，讚嘆不已阿！